Astronomia podczas przygotowań do matury jest często tematem zaniedbywanym i traktowanym odrobinę po macoszemu. Często zamiast przerobić materiał z astronomii, który pojawi się na maturze - wolimy po raz kolejny powtórzyć dobrze już znany materiał z innych działów. A to błąd! Zadania z astronomii odpowiadają średnio za 6 punktów na maturze z fizyki. Co więcej to są punkty, które łatwo zdobyć!
Astronomia może wydawać się trudna, ale są to tylko pozory. Tak naprawdę absolutną większość astronomii maturalnej można zamknąć w czterech działach - grawitacja, orbity, zasady zachowania, paralaxa. Czytając ten artykuł zapoznasz się z każdym z tych czterechdziałów, a pod koniec będziesz gotowa/gotów, by samodzielnie stawić czoła zadaniom maturalnym. Zatem do dzieła!
Grawitacja
Każdy z nas zapewne zna historię o Newtonie, który obserwując spadające jabłka wpadł na genialną hipotezę, że siła powodująca spadanie jabłka na Ziemię - to dokładnie ta sama siła, która utrzymuje księżyc na orbicie. Po krótkich obliczeniach udowodnił, że jego hipoteza zgadza się z rzeczywistością, a siła grawitacji działająca na jabłko, czy księżyc wyraża się wzorem:
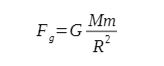
gdzie:
G - stała grawitacji - jest to liczba taka sama w całym wszechświecie, której wartość wynikaznaszej definicji jednostek SI (takich jak kilogram, metr czy sekunda).
M,m - masy oddziałujących ciał. W przypadku Ziemi przyciągającej jabłko - będą to masy jabłka oraz Ziemii.
R - odległość między środkami masy ciał. W przypadku Ziemi przyciągającej jabłko - będzie to odległość środka jabłka od środka Ziemi.
Były to narodziny naszego rozumienia o grawitacji.
Wzór Newtona poprawnie opisuje oddziaływanie mas punktowych, czyli ciał o rozmiarach znacznie mniejszych niż odległość między nimi. Przykładowo oddziaływanie między Ziemią a samochodem wystrzelonym w przestrzeń kosmiczną przez Elona Muska jest opisywane przez wzór Newtona. Choć zarówno Ziemia jak i samochód są całkiem duże - to w porównaniu z odległością między nimi wydają się malutkie.
źródło: grafika własna
źródło: https://en.wikipedia.org/wiki/Elon_Musk%27s_Tesla_Roadster
A co w przypadku wspomnianego na początku rozdziału jabłka? Przecież nie możemy powiedzieć, że rozmiary jabłka i Ziemi są znacznie mniejsze od odległości jabłka od środka Ziemi. Tutaj z pomocą przychodzi nam pewien szczęśliwy, matematyczny zbieg okoliczności. Mianowicie wzór Newtona można stosować również do ciał sferycznie symetrycznych, takich jak Ziemia. Zatem oddziaływanie pomiędzy Ziemią, a jabłkiem, bananem, człowiekiem, czy samochodem również będzie opisane za pomocą wzoru Newtona. Jednak oddziaływanie między samochodem, a człowiekiem w samochodzie już nie będzie opisane takim wzorem ponieważ nie są to działa sferycznie symetryczne i niemożemy ich traktować jako ciała punktowe (ponieważ są zbyt blisko siebie).
źródło: grafika własna
Pozostaje jeszcze jedno pytanie. W szkole uczyliśmy się o wzorze opisującym siłę grawitacji między Ziemią, a dowolnym ciałem na Ziemi przyjmującym następującą postać:
Fg = mg
gdzie:
g - przyspieszenie grawitacyjne (inne dla każdej planety)
m - masa ciała, na które w wyniku oddziaływania z Ziemią działa siła grawitacji. Żeby ustalić co się dzieje, czemu mamy dwa wzory na to samo porównajmy je ze sobą:
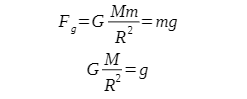
Z przyrównania tych wzorów wyprowadziliśmy wyrażenie na przyspieszenie grawitacyjne g -zależy ono od masy Ziemi M, odległości ciała od Ziemi (czyli w przybliżeniu jej promienia R)oraz stałej grawitacyjnej G. Warto zapamiętać to wyprowadzenie!
Energia Potencjalna
Wiemy już jak obliczyć siłę grawitacji, a co z energią potencjalną? Z wzoru Newtona można wywnioskować, że energia potencjalna oddziaływania grawitacyjnego ciał punktowych (lub sferycznie symetrycznych) dana jest wzorem:
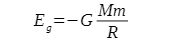
wygląda ona bardzo podobnie do wzoru na siłę. Brakuje jedynie kwadratu w mianowniku i pojawia się tajemniczy znak - .Podobnie jak w przypadku siły - możemy chcieć wyrazić energię potencjalną za pomocą przyspieszenia grawitacyjnego g. Otrzymamy wtedy dobrze znany wzór:
Eg=−mg h
Uwaga! Pamiętaj, że wzory Eg=−mgh i Fg=mg możemy stosować do opisania oddziaływania dowolnego ciała z Ziemią pod warunkiem, że ciało to nie jest za daleko od powierzchni Ziemi. W przypadku samochodu Tesli musimy już użyć wzorów: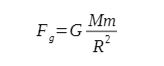i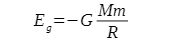
Zadanie 4 matura czerwiec 2018
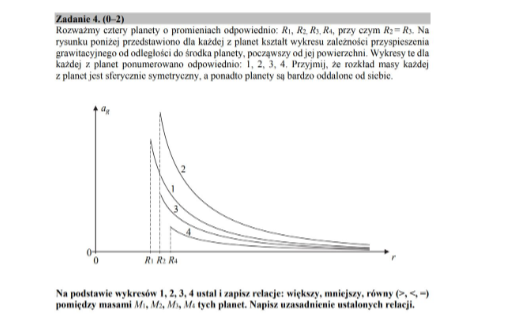
źródło: https://arkusze.pl/maturalne/fizyka-2018-czerwiec-matura-rozszerzona.pdf
Na osi y mamy przyspieszenia grawitacyjne w pewnej odległości od planety. Wyrażenie naprzyspieszenie grawitacyjne w odległości r od środka planety to:
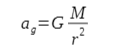
Widzimy zatem, że jeśli weźmiemy kilka planet i zmierzymy przyspieszenie grawitacyjne na każdej z nich w identycznej odległości r od ich środka - to otrzymamy tym większą wartość przyspieszenia ag im większa jest masa planety
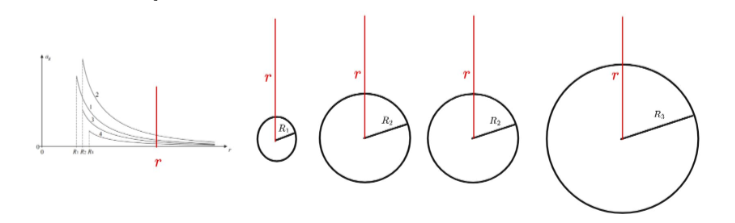
źródło: grafika własna
Widzimy zatem z wykresu, że ag2(r)>ag1(r)>ag3(r)>ag4(r), a stąd dostajemy, że M2>M1>M3>M4.
Orbity
Jak pewnie wiesz, zgodnie z I prawem Keplera planety podlegające sile grawitacji poruszają się po eliptycznych orbitach. To właśnie dzięki temu prawu Newton był w stanie wyprowadzić swój wzór.
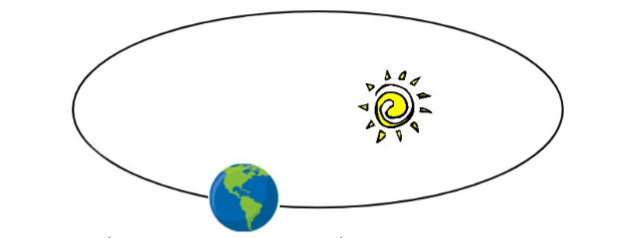
źródło: grafika własna
Ciężko jest liczyć orbity eliptyczne. Na szczęście na maturze zwykle wystarcza nam swoboda w analizie orbit kołowych (koło to szczególny przypadek elipsy). Porozmawiajmy zatem o orbitach kołowych. Aby ciało poruszało się po okręgu musi pojawić się pewna siła dośrodkowa. Jest ona dana równaniem:
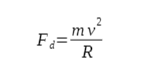
gdzie:
m- to masa ciała poruszającego się po okręgu,
R- promień okręgu po którym porusza się ciało,
v- jego prędkość.
Siła odśrodkowa powoduje, że ciało cały czas zmienia kierunek swojej prędkości i pozostaje na trajektorii okrężnej. Jeśli złapiemy jeden koniec kabla od ładowarki i zaczniemy nim kręcić- siłą dośrodkową, która sprawi, że drugi koniec ładowarki będzie poruszał się po okręgu będzie siła naprężenia kabla.
W przypadku samochodu poruszającego się po rondzie - siłą dośrodkową będzie siła tarcia opon o podłoże, a dla planety poruszającej się po okręgu dookoła słońca taką siłą będzie siła grawitacji. Skoro siła grawitacji dla planety jest siłą dośrodkową to możemy zapisać:
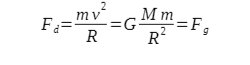
Stąd możemy wywnioskować że:
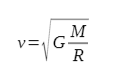
Widać zatem, że ciało poruszające się po orbicie wokół gwiazdy o masie będzie miało konkretną prędkość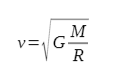
Jeśli prędkość ciała będzie inna niż to nie będzie ono się poruszało po orbicie kołowej, tylko po orbicie eliptycznej. Zwróć uwagę, że prędkość orbitowania nie zależy od masy orbitującej ciała m.
źródlo: grafika własna
Ważna definicja:
Pierwsza prędkość kosmiczna to prędkość jaką należy nadać ciału, aby poruszało się ono po orbicie o promieniu równym promieniowi planety.
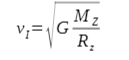
Jeśli mówimy o pierwszej prędkości kosmicznej dla Ziemi, to to masa Ziemi, to promień Ziemi, a .
Zasady zachowania
Zasady zachowania, takie jak zasada zachowania energii, czy momentu pędu mają na celu ułatwić nam życie i robią to bardzo skutecznie. Dzięki nim możemy znacząco uprościć rozwiązanie zadania, jednak zasady zachowania mają też mroczną stronę - nie działają zawsze.
Zasady zachowania działają tylko wtedy, gdy nasz układ jest izolowany, czyli gdy nie oddziałuje z innymi ciałami. O układzie możemy powiedzieć, że jest izolowany, gdy jego zachowanie się nie zmieni - jeśli pozbędziemy się z naszego wszechświata wszystkiego, co nie należy do układu. Przykładowo Ty nie jesteś układem izolowanym ponieważ gdybyśmy pozbyli się wszystkiego poza Tobą z naszego wszechświata - Twoje zachowanie znacząco się zmieni - bez atmosfery zaczniesz się dusić, a Twoja temperatura zacznie powoli spadać ponieważ nie będzie słońca, czy Ziemi, które mogłyby dostarczyć Ci ciepła. Jednak jeśli jako układ weźmiemy: słońce, Ziemię i Ciebie to już będzie znacznie lepszym układem izolowanym, jeśli pozbylibyśmy się wszystkiego innego - to z Twojej perspektywy niewiele się zmieni. Szczęśliwie dla nas, zwykle w zadaniach astronomicznych układy są izolowane. Możemy zatem używać zasad zachowania.
Zasada zachowania energii
Całkowita energia w każdym momencie jest taka sama. Na całkowitą energię w zadaniach astronomicznych składa się energia kinetyczna i energia potencjalna każdego z ciał:
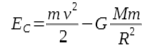
Zasada zachowania momentu pędu
Całkowity moment pędu w każdym momencie jest taki sam. Na całkowity moment pędu w zadaniach astronomicznych składa się moment pędu każdego z ciał:
Lc = mvr
gdzie:
m - masa ciała, którego momentu pędu szukamy,
R - jego odległość od osi obrotu,
v - składowa prędkości prostopadła do promienia.
Zadanie 15 matura maj 2018
źródło: https://arkusze.pl/maturalne/fizyka-2019-maj-matura-rozszerzona.pdf
Aby rozwiązać to zadanie skorzystamy z zasady zachowania energii i porównamy energię Merkurego w peryhelium do jego energii w aphelium. Z treści zadania znamy rp, ra, va, oraz M.. Wyznaczenie vp sprowadza się zatem jedynie do prostego przekształcenia algebraicznego
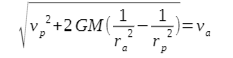
To zadanie można zrobić prościej!
W naszym układzie nie tylko energia jest zachowana, ale również moment pędu. Przyrównując moment pędu w peryhelium i aphelium dostajemy:
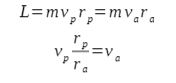
Ta metoda jest dużo prostsza ponieważ nie musimy zamieniać jednostek i na jednostki SI, co znacznie zmniejsza szanse popełnienia błędu.
Paralaksa
Gwiazda położona najbliżej Ziemi (poza słońcem) to Alfa Centauri. Znajduje się ona roku świetlnego od nas. Czyli w odległości jaką światło pokona w ciągu lat. Ale, czy zastanawiało Cię kiedyś, jak mierzymy „jak daleko” gwiazdy są od nas? Odpowiedź to paralaksa.
Zjawisko paralaksy polega na względnej zmianie położenia gwiazdy bliskiej nam, na tle gwiazd odległych. Jeśli wydaje Ci się to niejasne - zerknij na poniższy rysunek.
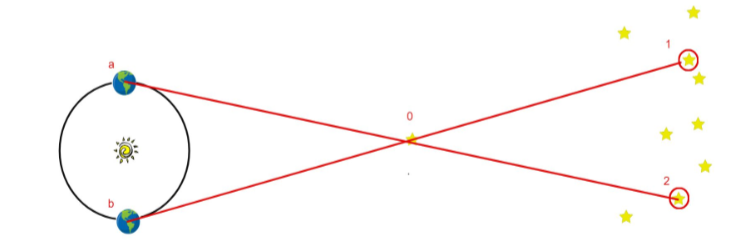
źródło: grafika własna
Kiedy patrzymy na gwiazdę 0 w momencie kiedy nasza planeta znajduje się w miejscu b na orbicie - to na tle odległych gwiazd zobaczymy gwiazdę 0 w położeniu 1. Jeśli teraz poczekamy pół roku na to aż nasza planeta przemieści się do położenia a - zobaczymy, że ta sama gwiazda 0 teraz będzie wydawała się zajmować położenie 2. Zobaczymy zatem, że gwiazda przemieściła się o pewien kąt . Jest to pozorne przemieszczenie, gwiazda tak naprawdę nigdzie się nie ruszyła, to my się przemieściliśmy. Z pozornego przemieszczenia możemy odgadnąć odległość gwiazdy 0 od słońca.
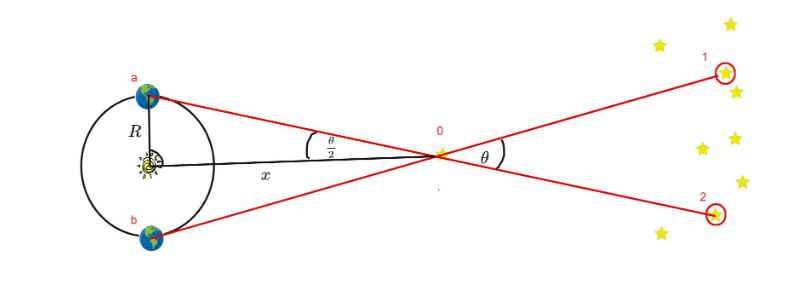
źródło: grafika własna
Z prostej geometrii wiemy, że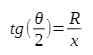 
zwykle kąt 0 jest bardzo mały (znacznie mniejszy od jednego stopnia). W takim przypadku możemy sobie jeszcze bardziej uprościć życie i skorzystać z przybliżenia małych kątów:
czyli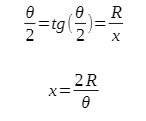 
Zakończenie
źródło: https://unsplash.com/photos/HUnKka6VtZc
I to już koniec. Na tym kończy się nasza podróż po świecie astronomii maturalnej. Moje gratulacje, że udało Ci się dotrwać do końca. Mam nadzieję że wiedza, którą dzisiaj zdobyłaś/zdobyłeś będzie dla Ciebie przydatna.
Jeśli potrzebujesz dodatkowej pomocy z fizyką, wpadnij na mój profil na e-korepetycjach: Bartosz Markowicz
